11291. Поделить
деньги
Гусейн и его младший брат нашли
на улице кошелек с n банкнотами. Поскольку владельца денег найти не
удалось, они решили разделить деньги между собой. Они поделили деньги между
собой так, чтобы каждому досталось одинаковое количество денег. В это время
могло остаться наименьшее количество денег, которое можно было оставить. Гусейн
забирает эти деньги, потому что он старший брат.
Определите сумму денег, которая
досталась Гусейну.
Вход. В первой строке записано целое
число n (1 ≤ n ≤ 500) – количество банкнот в
кошельке. В каждой из следующих строк указано одно целое положительное значение
ci – стоимость i-ой банкноты (в манатах). Известно,
что c1 + ... + cn ≤ 105.
Выход. Выведите сумму денег, которая
досталась Гусейну.
|
Пример
входа 1 |
Пример
выхода 1 |
|
5 4 2 3 1 10 |
10 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
4 3 17 2 19 |
22 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Пусть s1 – текущая сумма у
Гусейна, s2 – текущая сумма
у его брата. Будем считать, что s1 > s2. Если вдруг
станет s1 > s2, то просто
поменяем суммы между братьями.
Объявим массив dp такой что dp[i] содержит наибольшую
сумму денег такую что ее можно выдать Гусейну и брату чтобы получить s1 – s2 = i. Отметим, что
при этом dp[i] = s1 + s2. Например, для
первого теста:
·
dp[0] = 20: Гусейн = {1, 2, 3, 4}, брат = {10}, (1 + 2 + 3 + 4)
– 10 = 0;
·
dp[1] = 19:
Гусейн
= {10}, брат = {2, 3, 4}, 10 – (2 + 3 +
4) = 1;
·
dp[2] = 20: Гусейн = {1, 10}, брат = {2, 3, 4}, (1 + 10) – (2 +
3 + 4) = 2;
·
dp[3] = 17:
Гусейн
= {10}, брат = {3, 4}, (10) – (3 + 4)
= 3;
Например раздать
братьям сумму, большую чем 17, чтобы разница сумм у них была 3, невозможно.
Инициализируем массив
dp значениями -1 (dp[i] = -1 означает
что невозможно раздать банкноты так чтобы разница сумм у братьев была i). Изначально
положим dp[0]
= 0.
Будем
последовательно обрабатывать банкноты. Пусть (i – 1) банкнот уже обработано, текущей
является банкнота номер i стоимостью ci.
Перебираем
ячейки массива dp. Рассмотрим ячейку dp[j], для которой s1 – s2 = j и dp[j] = s1 + s2.
1. Выдадим банкноту номер i Гусейну. Тогда
выданная сумма денег станет равной s1 + s2 + ci = dp[j] + ci, а разность
сумм у братьев станет равной (s1 + ci) – s2 = j + ci. Если сумма dp[j] + ci окажется больше
dp[j + ci], то значение dp[j + ci] следует обновить:
dp[j + ci] = max(dp[j + ci], dp[j] + ci)
2. Выдадим банкноту номер i брату Гусейна.
Тогда выданная сумма денег станет равной s1 + s2 + ci = dp[j] + ci, а разность
сумм у братьев станет равной s1 – (s2 + ci) = j – ci. Если сумма dp[j] + ci окажется больше
dp[j – ci], то значение dp[j – ci] следует обновить.
Однако может оказаться, что j – ci < 0. В таком случае
братья меняются деньгами, а разность берем по модулю:
dp[| j – ci |] = max(dp[| j – ci |], dp[j] + ci)
После обработки
всех банкнот dp[0]
хранит
наибольшую сумму, которую можно поровну раздать братьям. Остаток выдаем
Гусейну. Пусть sum –
сумма
всех имеющихся денег. Тогда Гусейн получит dp[0] / 2 + (sum – dp[0]).
Пример
Пусть имеются n = 3 банкноты номиналами {3, 5, 2}. Рассмотрим как будет изменяться состояние массива
dp по мере обработки банкнот.
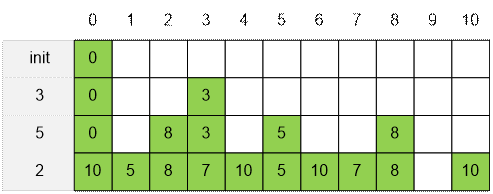
Рассмотрим обработку
массива для последней банкноты ci = 2.
·
Банкнота дается Гусейну, проход слева направо:
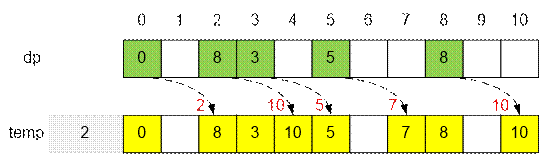
·
Банкнота дается брату Гусейна, проход справа налево:
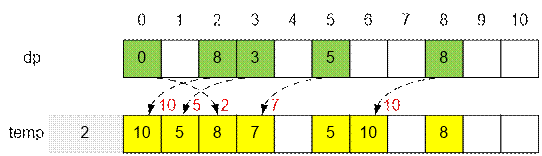
Для получения финального
результата следует найти максимум среди соответствующих ячеек массивов temp:

Реализация алгоритма
Читаем
количество банкнот n.
scanf("%d", &n);
Инициализируем
массивы значением -1.
#define MAX 100005
dp = vector<int>(MAX, -1);
tmp_dp = vector<int>(MAX, -1);
dp[0] = tmp_dp[0] = 0;
В
переменной sum вычисляем общую сумму денег.
sum = 0;
for (i = 0; i < n; i++)
{
Читаем
стоимость i-ой банкноты c. Прибавляем ее значение к общей сумме sum.
scanf("%d", &c);
sum += c;
Выдаем
банкноту стоимостью c брату Гусейна. Двигаемся справа
налево.
for (j = MAX - 1; j >= 0; j--)
if (dp[j] != -1)
tmp_dp[abs(j - c)] = max(tmp_dp[abs(j - c)], dp[j] + c);
Выдаем
банкноту стоимостью c Гусейну. Двигаемся слева направо.
for (j = 0; j < MAX - c; j++)
if (dp[j] != -1)
tmp_dp[j + c] = max(tmp_dp[j + c], dp[j] + c);
Копируем
содержимое массива tmp_dp в dp.
dp = tmp_dp;
}
Выводим
ответ.
printf("%d\n", dp[0] / 2 + (sum - dp[0]));